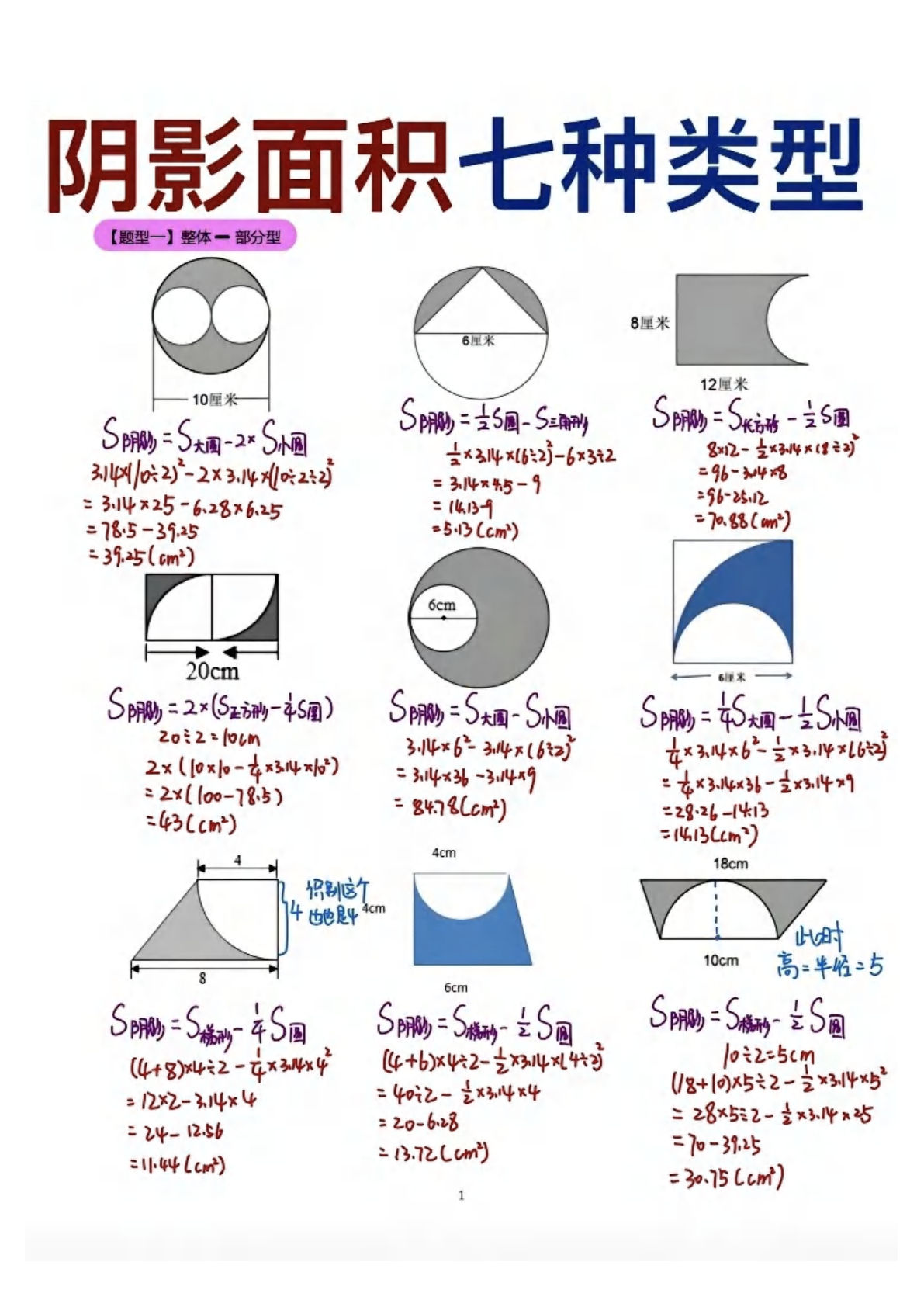
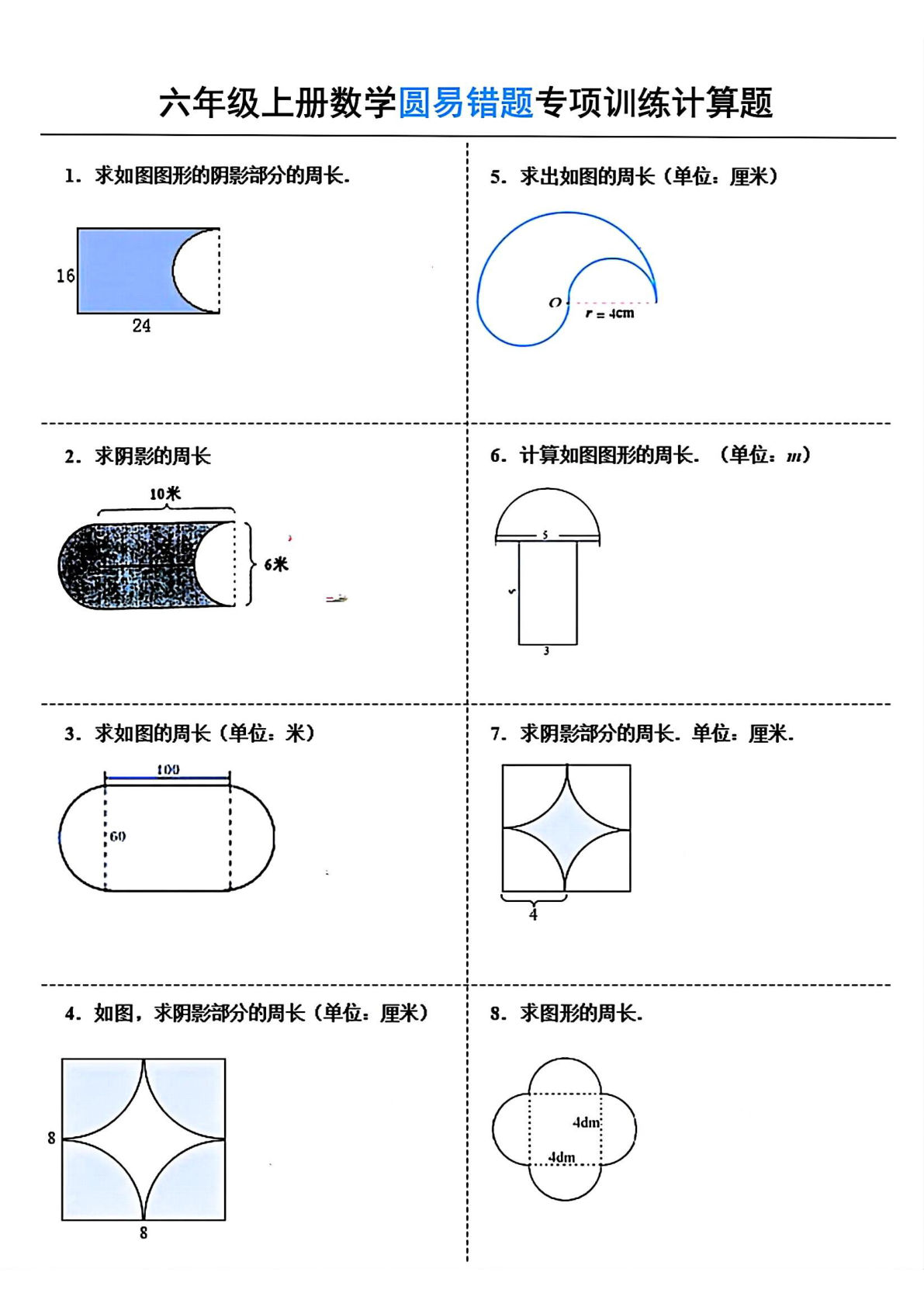
小学数学阴影面积七种解题技巧
这份阴影面积专项训练系统梳理了七类经典题型,通过整体减部分法、平移转化法等核心方法,帮助小学生掌握几何图形面积计算的精髓。
核心题型解析
整体减部分法:正方形内阴影面积计算
已知正方形边长为4厘米,阴影面积=正方形面积-空白部分面积
S阴影 = 4×4 - π×2² = 16 - 12.56 = 3.44(cm²)
圆环面积计算:阴影面积推导圆环面积
已知阴影面积为25m²,求圆环面积
R² - r² = 25×2 = 50 → S圆环 = π(R²-r²) = 3.14×50 = 157(m²)
半圆阴影问题:利用整体法求解
已知半圆面积12.56cm²,求阴影三角形面积
r² = 12.56×2÷3.14 = 8 → S阴影 = 8÷2 = 4(cm²)
四大训练优势
1. 方法体系完整:覆盖整体减部分、平移转化、等积变形等七种解题思路
2. 变量代换技巧:将R²-r²作为整体处理,避免复杂开方运算
3. 分步计算演示:每道题展示关键推导步骤,如半圆问题中r²的求法
4. 生活应用结合:包含花坛、圆环等实际场景的面积计算
使用建议
阶梯式训练:从基础的整体减部分法开始,逐步过渡到复杂的圆环面积计算
错题归类:将错误分为公式错误、计算错误、方法错误三类针对性改进
举一反三:掌握圆环面积公式后,可延伸思考椭圆环、不规则环形面积
这份阴影面积解题宝典特别适合:
- 五年级升六年级暑期衔接
- 小升初几何专题突破
- 奥数竞赛基础训练