 ...](http://jiwatiku.cn/content/uploadfile/202507/26621753806179.png)
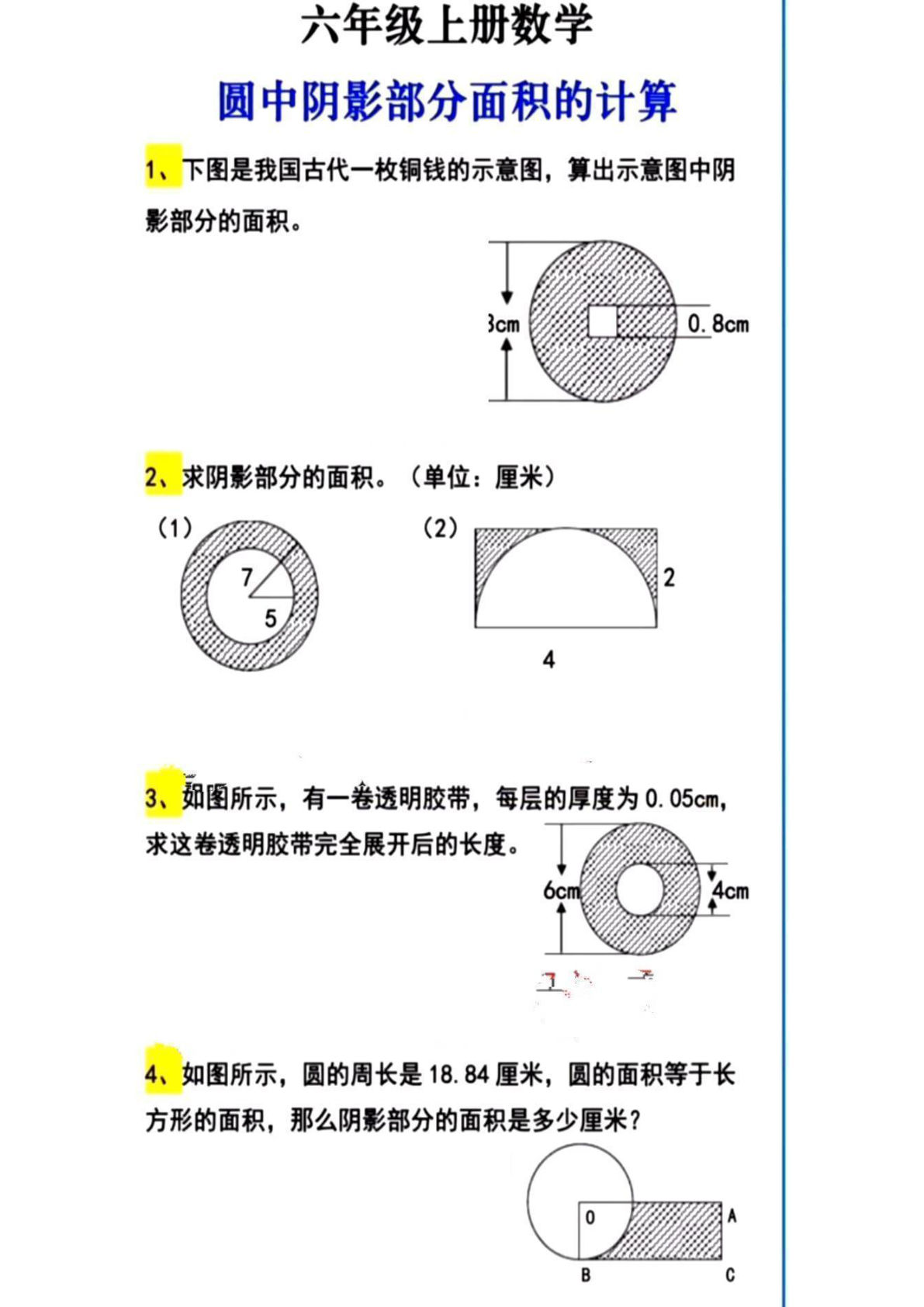
小学数学阴影面积十大解题技巧
这份阴影面积专项训练包含18种经典题型，系统讲解割补法、整体减部分、平移旋转等核心方法，是提升几何解题能力的必备资料。
三大核心解题方法
割补法：通过图形重组简化计算
例题八：将右上阴影补到左下空白
关键步骤：S阴=1/4πr²=3.14cm²
整体减部分：用规则图形面积相减
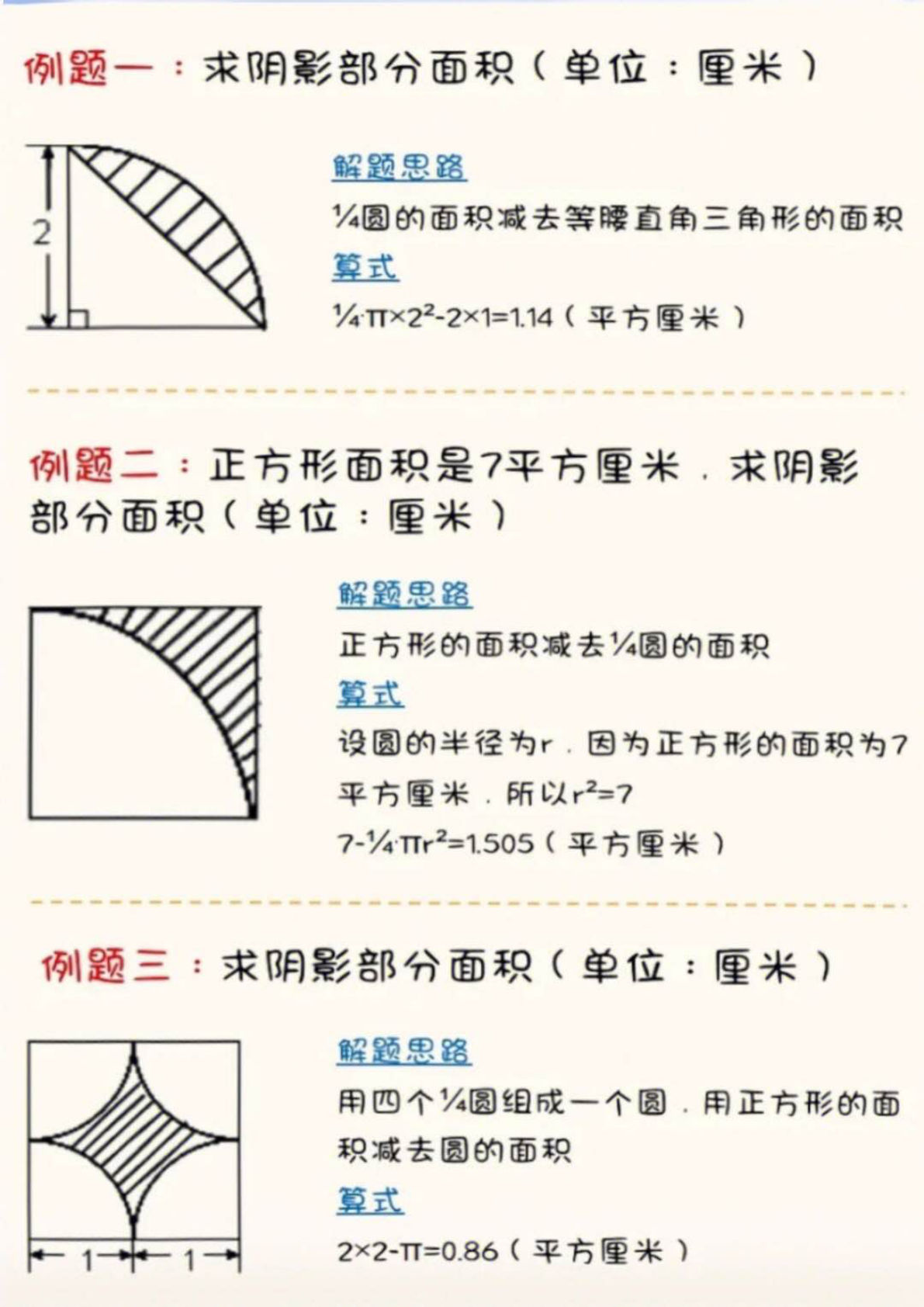
例题三：正方形减四分之一圆
计算公式：S阴=a²-πr²=0.86cm²
平移旋转法：利用对称性重组图形
例题九：平移阴影组成长方形
结果：S阴=长×宽=6cm²
五大特色题型
1. 叶形面积计算：例题五用双圆减正方形求"叶形"
2. 环形面积应用：例题六通过大圆减小圆求差值
3. 对角线妙用：例题七用对角线求正方形面积
4. 组合图形拆分：例题十二将三部分拼成半圆
5. 复杂图形简化：例题十七通过翻转转化为梯形
解题技巧精要
公式逆向运用：如例题二用正方形面积反推圆半径
等量代换思想：例题十通过面积等效平移计算
分步验证方法：例题十六分步计算三个圆的面积关系
这份几何阴影面积突破训练特别适合：
- 五年级升六年级暑期衔接
- 小升初几何专题强化
- 奥数竞赛图形专项训练
